2D 카테시안 좌표계에서 점 입자의 운동

엔진에서 어떤 물리 시스템(계)을 시뮬레이션하려면, 수치 해석적으로 접근해야 되고, 시간에 관한 함수로 나타낼 수 있어야 한다.

2차원 좌표계에서, 한 입자의 시간에 따른 위치를 r(t)라고 하겠다.

$$r(t) = x(t)\hat{i} + y(t)\hat{j}$$

위치를 미분하게 되면, 속도가 된다. 
$$v(t) = \dot{r} = \dot{x} + \dot{y}$$

거리가 s라면, 속력은 다음과 같다. 
$$\vert v \vert = \dot{s} = {ds \over dt}$$

가속도는 다음과 같다.
$$a(t) = \dot{v}= \ddot{r} = \ddot{x}\hat{i}+\ddot{y}\hat{j}$$

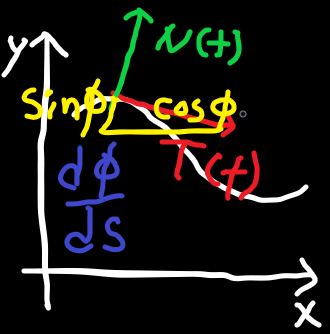
탄젠셜 벡터(접선 벡터)를 T, 노멀 벡터(법선 벡터)를 이라고 한다면
$$T(t) ={v \over \vert v \vert} = cos(\phi(t))\hat{i} + sin(\phi(t))\hat{i}$$
$$N(t) = -sin(\phi(t))\hat{i} + cos(\phi(t))\hat{i}$$

이제 속도를 탄젠셜 벡터를 통해서 나타낼 수 있다. 이때, 속도의 절댓값은 속력이 된다.

$$v = \vert v \vert = \dot{s}T$$

가속도도 구렁이 담 넘어가듯이, 나타내면 다음과 같다.

$$a = \dot{v} = {d(\dot{s}T)\over dt}$$
$$={d\dot{s} \over dt}T + \dot{s}{dT\over dt}$$
$$=\ddot{s}T + \dot{s}{dT\over ds}{ds\over dt}$$
$$=\ddot{s}T + \dot{s}^2{dT\over ds}$$

탄젠셜 벡터를 이동거리에 의해서 미분을 하게 되면, 노멀 벡터가 된다. 이때, 미소 이동거리에 대한 미소 각 팩터는 '곡률'이라고 할 수 있겠다..

$${dT \over ds} = {d\over ds}(cos\phi , sin\phi) = {d\phi \over ds}({cos\phi\over d\phi},{sin\phi\over d\phi}) = {d\phi\over ds}(-sin\phi, cos\phi) = {d\phi \over ds}N = \kappa N$$
$$where, \kappa = {d\phi\over ds}$$
$$a = \ddot{s}T + \dot{s}^2(\kappa N) = \ddot{s}T + \kappa \dot{s}^2N$$

$${dN\over ds} = {d\over ds}(-sin\phi, cos\phi) = {d\phi\over ds}(-cos\phi , sin\phi) = -\kappa $$

꿀팁으로 컴퓨터가 계산하기 쉽게, 행렬로 나타 낼 수 있다.

$$\begin{bmatrix}{dT \over ds} \\{dN \over ds} \end{bmatrix} = \begin{bmatrix}0 & \kappa \\ -\kappa & 0 \end{bmatrix}\begin{bmatrix} T \\ N\end{bmatrix}$$