2D 극좌표계에서 점 입자의 운동

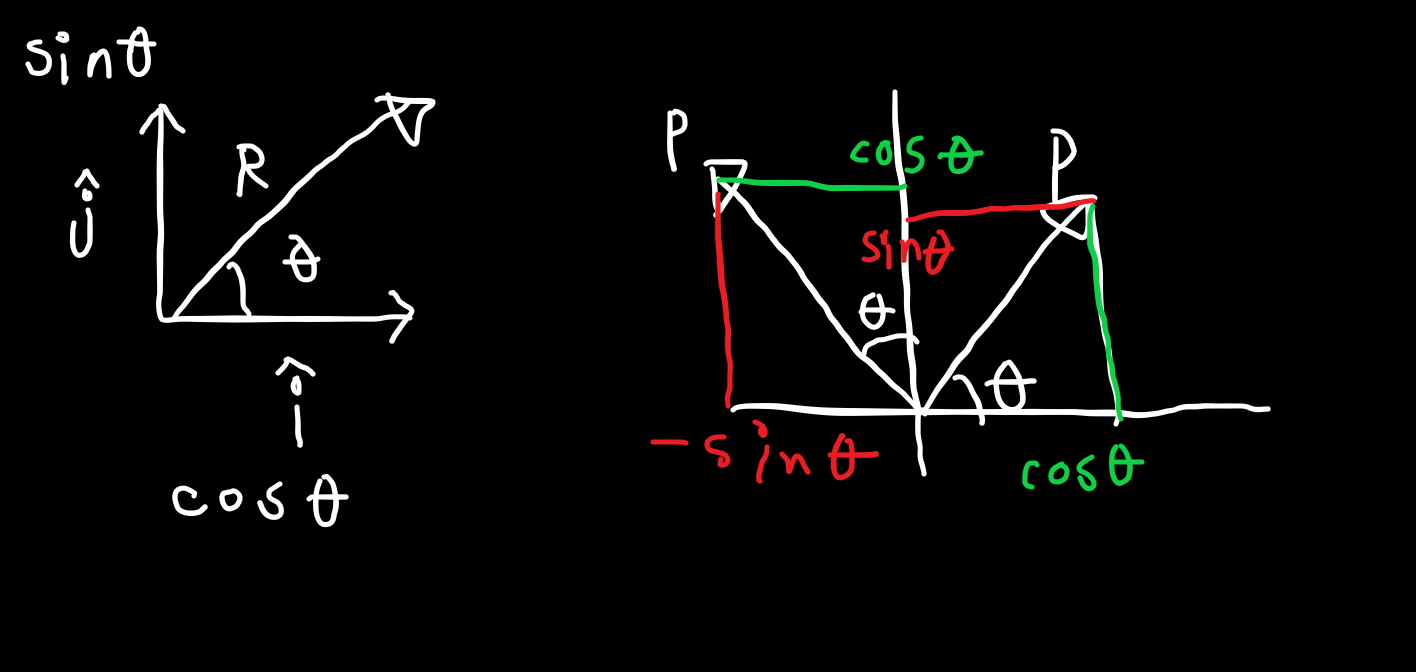
극좌표계에서 좌표는 중심각(theta)과 원점에서부터의 거리(R)로 좌표를 표현한다. 카테시안 좌표계의 x축을 R, y축을 P로 대응하면 서로 변환할 수 있음을 알 수 있다.

$$r = \vert r \vert R = r(cos\theta, sin\theta)$$
$$\dot{P} = \dot\theta P, \dot{P} = -\dot\theta R$$

P는 R을 -90도만큼 쉬프트한 벡터이기 때문에, 다음과 같은 관계가 성립한다.

$$\begin{bmatrix}\dot{R}\\ \dot{P} \end{bmatrix} = \begin{bmatrix}0 & \dot \theta \\ -\dot \theta & 0 \end{bmatrix} \begin{bmatrix} R \\ P\end{bmatrix}$$

속도는 다음과 같다.

$$v = \dot{r} = {d\over dt}(rR) = \dot{r}R + r\dot{R} = \dot{r}R + r\dot{\theta}P$$

가속도는 다음과 같다.

$$a = \dot{v} = {d \over dt}(\dot{r}R + r\dot{\theta}P)$$
$$= \ddot{r}R + \dot{r}\dot{R} + {d\over dt}(r\dot{\theta})P +r\dot{\theta}\dot{P}$$
$$=\ddot{r}R + \dot{r}\dot{\theta}P + (\dot{r}\dot{\theta} + r \ddot{\theta})P - r\dot{\theta}^2R$$
$$=(\ddot{r}- r\dot{\theta}^2)R + (r\ddot{\theta}+ 2\dot{r}\dot{\theta})P$$