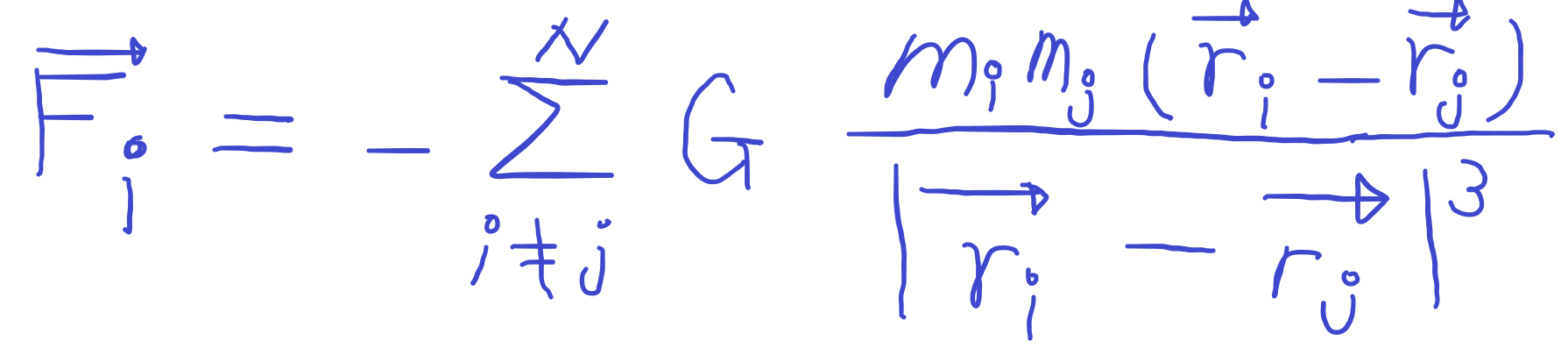
태양계는 8개의 행성과 그 행성들의 위성들, 그리고 소행성 벨트와 카이퍼 벨트로 이루어져 있다. 태양계의 모든 천체를 시뮬레이션하기 어렵기 때문에, 9-body 시스템이라 생각한다.
- 뉴턴의 중력법칙에 따라, 외력이 없다면, i 번째 물체에 작용하는 힘은 요런 식이다. 여기서, i는 i 번째 행성, j는 태양이라고 하면, 8+7+6+5+4+3+2+1 개의 힘을 계산해야 한다. 단순히 행성 간의 중력은 무시한다고 하면, 8번 만으로 족하지만, 겉멋을 중요시하기 때문에 모두 계산한다. 그리고 이 힘을 가지고, 매 frame 마다, 행성의 위치를 업데이트시켜 준다.


- 태양계가 만들어진 조건은 완전 운빨이다. 각각의 천체의 mass, distance, orbital velocity 가 조금이라도 어긋나면, 행성은 태양으로 빨려 들어간다. 9-body 시스템을 만드는데, 주먹구구식으로 값을 입력하면서, 행성이 공전을 하는지 확인하는 것을 불가능하다. 그래서 nasa planet table ratio를 참고한다. 내가 정리한 값은 다음과 같다.
| Ratio to Earth Values | ||||
| Planet | Mass | Distance from Sun | Orbital Velocity | Orbital Period |
| Mercury | 0.0553 | 0.387 | 1.59 | 0.251 |
| Venus | 0.815 | 0.723 | 1.18 | 0.615 |
| Earth | 1 | 1 | 1 | 1 |
| Mars | 0.107 | 1.52 | 0.808 | 1.88 |
| Jupiter | 317.8 | 5.20 | 0.439 | 11.9 |
| Saturn | 95.2 | 9.58 | 0.325 | 29.4 |
| Uranus | 14.5 | 19.20 | 0.228 | 83.7 |
| Neptune | 17.1 | 30.05 | 0.182 | 163.7 |
- 여기서 Orbital Period를 가지고, 케플러 법칙을 만족하는지 볼것이다. 케플러 법칙은 결국에 에너지 보존 법칙이기 때문에, 시뮬레이션한 모델이 유효한가의 척도가 된다. 만약, 시뮬레이션이 유효하지 않다면, 행성은 몇 번의 연산만에 태양 속으로 빨려 들어간다. 원인은 다양하다.
- 언어 자체의 한계 : 예를 들어, 어떤 언어는 Double Precision을 지원하지 않는다. 하지만 파이썬은 지원!
- 메소드 선택의 문제 : Euler, Heun, LeapFrog, MidPoint, Modified Euler 메서드는 작은 타임 스텝에서 부정확하다.
- Rounding, Chopping 등등
- 케플러 법칙 : T를 행성의 공전주기, R을 Orbital Distance라고 한다면, 케플러 법칙에 따라, 다음이 성립한다. 즉, Orbital Velocity 와 Square Root of Distance from Sun를 곱한 값이, 1에 가까울수록 정확한 것이다.

- RK4와 파이썬으로 작성한 나의 코드는 다음과 같다.
#Copyright Young il
def partial_step(a, b, time_step):
ret = vector(0,0,0)
ret.x = a.x + b.x * time_step
ret.y = a.y + b.y * time_step
ret.z = a.z + b.z * time_step
return ret
def acc(p1,p2):
k1 = vector(0,0,0)
k2 = vector(0,0,0)
k3 = vector(0,0,0)
k4 = vector(0,0,0)
acc = vector(0,0,0)
# Calculate the gravitational acceleration exerted on p1 by p2.
G = 6.67e-11
# Calculate distance vector between p1 and p2.
r_vec = p1.pos-p2.pos
r_mag = mag(r_vec)
r_hat = r_vec/r_mag
tmp = G * p2.mass / r_mag**3
k1.x = tmp * (p2.pos.x - p1.pos.x)
k1.y = tmp * (p2.pos.y - p1.pos.y)
k1.z = tmp * (p2.pos.z - p1.pos.z)
tmp_vel = partial_step(p1.velocity, k1, 0.5)
tmp_loc = partial_step(p1.pos, tmp_vel, 0.5*dt)
k2.x = (p2.pos.x - tmp_loc.x) * tmp
k2.y = (p2.pos.y - tmp_loc.y) * tmp
k2.z = (p2.pos.z - tmp_loc.z) * tmp
tmp_vel = partial_step(p1.velocity, k2, 0.5)
tmp_loc = partial_step(p1.pos, tmp_vel, 0.5 * dt)
k3.x = (p2.pos.x - tmp_loc.x) * tmp
k3.y = (p2.pos.y - tmp_loc.y) * tmp
k3.z = (p2.pos.z - tmp_loc.z) * tmp
tmp_vel = partial_step(p1.velocity, k3, 1)
tmp_loc = partial_step(p1.pos, tmp_vel, dt)
k4.x = (p2.pos.x - tmp_loc.x) * tmp;
k4.y = (p2.pos.y - tmp_loc.y) * tmp;
k4.z = (p2.pos.z - tmp_loc.z) * tmp;
acc.x += (k1.x + k2.x * 2 + k3.x * 2 + k4.x) / 6;
acc.y += (k1.y + k2.y * 2 + k3.y * 2 + k4.y) / 6;
acc.z += (k1.z + k2.z * 2 + k3.z * 2 + k4.z) / 6;
return acc
# planet and orbital data from:
# http://nssdc.gsfc.nasa.gov/planetary/factsheet/planet_table_ratio.html
# http://www.sjsu.edu/faculty/watkins/orbital.html
#mE is [earth mass] in kg
#vE is [Orbital velocity] in km/s
#dE is [Orbital distance]*10 in km
#rE is imaginary [Earth Radius]
mE = 5.97e24
vE = 30e3
dE = 149.6e9
rE = 696e6
sun = sphere( pos=vector(0,0,0), radius=33*rE, texture = "http://i.imgur.com/yoEzbtg.jpg",
mass = 333000 * mE, velocity = vector(0,0,0), make_trail=True,opacity = 0.8,
emissive = True)
mercury = sphere( pos=vector(0.387 * dE,0,0), radius=0.383*rE, texture = "https://i.imgur
.com/Qt5vzSi.jpg",
mass = 0.0553 * mE, velocity = vector(0,0,1.607 * vE), make_trail=True,
trail_color = color.yellow)
venus = sphere( pos=vector(0.723 * dE,0,0), radius=0.949*rE, texture = "https://i.imgur.com
/yJb167w.jpg",
mass = 0.815 * mE, velocity = vector(0,0,1.174 * vE), make_trail=True ,
trail_color = color.orange)
earth = sphere( pos=vector(dE,0,0), radius=rE, texture = "http://i.imgur.com/rhFu01b.jpg",
mass = mE, velocity = vector(0,0,vE) ,make_trail=True,
trail_color = color.cyan)
mars = sphere( pos=vector(1.52 * dE,0,0), radius=0.532*rE, texture = "https://i.imgur.com/
lMiiNCV.jpg",
mass = 0.107 * mE, velocity = vector(0,0,0.802 * vE), make_trail=True ,
trail_color = color.magenta)
jupiter = sphere( pos=vector(5.20 * dE,0,0), radius=11.21*rE, texture = "https://i.imgur.
com/boLfPBR.jpg",
mass = 317.8 * mE, velocity = vector(0,0,0.434 * vE), make_trail=True ,
trail_color = color.purple)
saturn = sphere( pos=vector(9.58 * dE,0,0), radius=9.45*rE, texture = "https://i.imgur.com
/RniHEKA.jpg",
mass = 95.2 * mE, velocity = vector(0,0,0.323 * vE), make_trail=True,
axis = vector(0.7, 1, 0), trail_color = color.blue)
uranus = sphere( pos=vector(19.20 * dE,0,0), radius=4.01*rE, texture = "https://i.imgur.com
/JFdN4ms.jpg",
mass = 14.5 * mE, velocity = vector(0,0,0.228 * vE,), make_trail=True,
trail_color = color.green)
neptune = sphere( pos=vector(30.05 * dE,0,0), radius=3.88*rE, texture = "https://i.imgur.com
/OnYEetD.jpg",
mass = 17.1 * mE, velocity = vector(0,0,0.182 * vE), make_trail=True, retain = 250 ,
trail_color = color.red)
sunlight = local_light( pos = sun.pos, color=color.white)
saturn_ring = ring(axis = vector(-0.7, 1, 0), size = vec(saturn.radius*0.1, saturn.radius*3,
saturn.radius*3))
moon = sphere (radius = earth.radius * 0.27, texture = "http://i.imgur.com/YPg4RPU.jpg",
make_trail=True, trail_color = color.white)
scene.camera.follow(sun) # have the camera default to centering on the sun
RotateSpeed = 0.00002
t=0
dt = 1000
dis_graph = graph(xtitle="Time",ytitle="Distance From the Sun")
mercury_dis = gcurve(label="Mercury", color= color.black, graph=dis_graph)
venus_dis = gcurve(label="Venus", color= color.orange, graph=dis_graph)
earth_dis = gcurve(label="Earth", color= color.cyan, graph=dis_graph)
mars_dis = gcurve(label="Mars", color= color.magenta, graph=dis_graph)
jupiter_dis = gcurve(label="Jupiter", color= color.purple, graph=dis_graph)
saturn_dis = gcurve(label="Saturn", color= color.blue, graph=dis_graph)
uranus_dis = gcurve(label="Uranus", color= color.green, graph=dis_graph)
neptune_dis = gcurve(label="Neptune", color= color.red, graph=dis_graph)
speed_graph = graph(xtitle="Time",ytitle="Orbital Speed")
mercury_vel = gcurve(label="Mercury", color= color.black, graph=speed_graph)
venus_vel = gcurve(label="Venus", color= color.orange, graph=speed_graph)
earth_vel = gcurve(label="Earth", color= color.cyan, graph=speed_graph)
mars_vel = gcurve(label="Mars", color= color.magenta, graph=speed_graph)
jupiter_vel = gcurve(label="Jupiter", color= color.purple, graph=speed_graph)
saturn_vel = gcurve(label="Saturn", color= color.blue, graph=speed_graph)
uranus_vel = gcurve(label="Uranus", color= color.green, graph=speed_graph)
neptune_vel = gcurve(label="Neptune", color= color.red, graph=speed_graph)
while (True):
rate(1000000000)
#9 Body System
sun.acc = acc(sun,mercury) + acc(sun,venus) + acc(sun,earth) + acc(sun,mars) + acc(sun,jupiter)
+ acc(sun,saturn) + acc(sun,uranus) + acc(sun,neptune)
mercury.acc = acc(mercury,sun) + acc(mercury,venus) + acc(mercury,earth) + acc(mercury,mars)
+ acc(mercury,jupiter) + acc(mercury,saturn) + acc(mercury,uranus) + acc(mercury,neptune)
venus.acc = acc(venus,sun) + acc(venus,mercury) + acc(venus,earth) + acc(venus,mars)
+ acc(venus,jupiter) + acc(venus,saturn) + acc(venus,uranus) + acc(venus,neptune)
earth.acc = acc(earth,sun) + acc(earth,mercury) + acc(earth,venus) + acc(earth,mars)
+ acc(earth,jupiter) + acc(earth,saturn) + acc(earth,uranus) + acc(earth,neptune)
mars.acc = acc(mars,sun) + acc(mars,mercury) + acc(mars,venus) + acc(mars,earth) + acc(mars,jupiter)
+ acc(mars,saturn) + acc(mars,uranus) + acc(mars,neptune)
jupiter.acc = acc(jupiter,sun) + acc(jupiter,mercury) + acc(jupiter,venus) + acc(jupiter,earth)
+ acc(jupiter,mars) + acc(jupiter,saturn) + acc(jupiter,uranus) + acc(jupiter,neptune)
saturn.acc = acc(saturn,sun) + acc(saturn,mercury) + acc(saturn,venus) + acc(saturn,earth)
+ acc(saturn,mars) + acc(saturn,jupiter) + acc(saturn,uranus) + acc(saturn,neptune)
uranus.acc = acc(uranus,sun) + acc(uranus,mercury) + acc(uranus,venus) + acc(uranus,earth)
+ acc(uranus,mars) + acc(uranus,jupiter) + acc(uranus,saturn) + acc(uranus,neptune)
neptune.acc = acc(neptune,sun) + acc(neptune,mercury) + acc(neptune,venus) + acc(neptune,earth)
+ acc(neptune,mars) + acc(neptune,jupiter) + acc(neptune,saturn) + acc(neptune,uranus)
# Update velocity
sun.velocity = sun.velocity + sun.acc*dt
mercury.velocity = mercury.velocity + mercury.acc*dt
venus.velocity = venus.velocity + venus.acc*dt
mars.velocity = mars.velocity + mars.acc*dt
jupiter.velocity = jupiter.velocity + jupiter.acc*dt
saturn.velocity = saturn.velocity + saturn.acc*dt
uranus.velocity = uranus.velocity + uranus.acc*dt
neptune.velocity = neptune.velocity + neptune.acc*dt
earth.velocity = earth.velocity + earth.acc*dt
# Update position
sun.pos = sun.pos + sun.velocity*dt
mercury.pos = mercury.pos + mercury.velocity*dt
venus.pos = venus.pos + venus.velocity*dt
mars.pos = mars.pos + mars.velocity*dt
jupiter.pos = jupiter.pos + jupiter.velocity*dt
saturn.pos = saturn.pos + saturn.velocity*dt
uranus.pos = uranus.pos + uranus.velocity*dt
neptune.pos = neptune.pos + neptune.velocity*dt
earth.pos = earth.pos + earth.velocity*dt
moon.pos = earth.pos + vector(earth.radius * 4 * cos(radians(t*0.0001)), 0,
earth.radius * 4 * sin(radians(t*0.0001)) )
saturn_ring.pos = saturn.pos
sunlight.pos = sun.pos
# plot values
mercury_dis.plot( pos=(t, mag(mercury.pos-sun.pos) ))
venus_dis.plot ( pos=(t, mag(venus.pos -sun.pos) ))
earth_dis.plot ( pos=(t, mag(earth.pos -sun.pos) ))
mars_dis.plot ( pos=(t, mag(mars.pos -sun.pos) ))
jupiter_dis.plot( pos=(t, mag(jupiter.pos-sun.pos) ))
saturn_dis.plot ( pos=(t, mag(saturn.pos -sun.pos) ))
uranus_dis.plot ( pos=(t, mag(uranus.pos -sun.pos) ))
neptune_dis.plot( pos=(t, mag(neptune.pos-sun.pos) ))
mercury_vel.plot( pos=(t, mag(mercury.velocity) ))
venus_vel.plot ( pos=(t, mag(venus.velocity ) ))
earth_vel.plot ( pos=(t, mag(earth.velocity ) ))
mars_vel.plot ( pos=(t, mag(mars.velocity ) ))
jupiter_vel.plot( pos=(t, mag(jupiter.velocity) ))
saturn_vel.plot ( pos=(t, mag(saturn.velocity ) ))
uranus_vel.plot ( pos=(t, mag(uranus.velocity ) ))
neptune_vel.plot( pos=(t, mag(neptune.velocity) ))
#update Time
t = t + dt
# rotate the earth 360 times per year
earth.rotate (angle = radians(-RotateSpeed * 360), axis = vec(0, 1, 0))
# the moon is in tidal lock so always shows the same face to Earth
moon.rotate (angle = radians(RotateSpeed * 13), axis = vec(0, 1, 0))
sun.rotate (angle = radians(-RotateSpeed * 16), axis = vec(0, 1, 0))
- dt를 1000으로 했을때, 이런 결과가 나왔다. 대충 1에 가까운 모습이다.
| Planet | √R | V | V * √R |
| Mercury | 0.622 | 1.59 | 0.989 |
| Venus | 0.850 | 1.18 | 1.00 |
| Earth | 1 | 1 | 1 |
| Mars | 1.23 | 0.808 | 0.996 |
| Jupiter | 2.28 | 0.439 | 1.00 |
| Saturn | 3.09 | 0.325 | 1.00 |
| Uranus | 4.38 | 0.228 | 0.999 |
| Neptune | 5.48 | 0.182 | 0.997 |