어떤 값을 테일러 시리즈로 전개하고 전개식으로 계산하면, 그 끝에서는 원래 값과 일치할까?
하지만 극한에 이르러서는 차이가 생기고, 이 차이가 완전히 다른 결과를 낳는다면?
컴퓨터로 어떤 값을 계산할 때, double형의 데이터를 int형으로 형 변환될 때, 소수점 뒤에 값은 날아간다.
이때, 그 값은 chopping 된 값이다. 반대로, 사람이 chopping 할 수도 있는데, 유효숫자를 고려하지 않고,
그냥 편의대로 소수점 몇 번째 자리는 무시하는 것이다. 아무튼... 수치해석에서는 반올림할 때,
우리가 통상적으로 알고 있던 방식으로 하지 않고, 마지막 수가 5라면, 그 위의 자릿수가 짝수가 오도록
내림/올림 한다. 가령, 1.45를 반올림하면, 1.5이지만, 수치해석에서는 1.4로 한다. 만약에 1.55라면, 맨 뒤 자리 수가
짝수가 와야 되므로, 1.6으로 한다. 이것을 Rounding 한다고 하며, 수치해석에서는 이것이 국룰이다.
아무튼... 수치해석은 다항식을 이해하는 것부터 시작한다.
다항식은 항이 여러 개인 친구다.
일찍이, 호너라는 작자는 다항식을 푸는 꼼수를 발견했는데, 이것을 사용하면, 컴퓨터의 연산 횟수를 줄일 수 있다.
예를 들어, {2, 6, 7, 5}라는 항이 있다 치자, 이식은 4차 방정식이다. 연산 횟수, 곱셈 3+2+1+1+1+1번 덧셈 1+1+1번이 들어간다.
하지만, 호너 씨의 알고리즘이라면, 7번이면 족하다. 당연히, 이 차이는 항이 많아질수록 심해질 것이다.
다항식, p를 호너식으로 수도 코드를 작성하면 다음과 같다.
integer p, n; real p, x;
real array a(0 to n)
p <- a[n]
for i = n-1 to 0
p = a[i] + x*p
end for사실, 호너 씨의 알고리즘은, 우리가 통상적으로 알고 있던 조립제법과 같다.
이것을 수도 코드로 작성하면 다음과 같다.
integer i, n; real r;
real array a(0 to n), b(0 to n-1)
b[n] <- a[n]
for i = n-1 to 0
b[i-1] = a[i] + r*b[i]
end for물론, 직접 코드를 작성할 때, 수도 코드처럼 인덱스를 1부터 시작하는 배열을 쓰거나, 내림차순으로 전개할 필요는 없다.
아무튼...컴퓨터는 값을 넣어주면, 답을 내놓는 똑똑한 친구이다. 미분도 할 수 있다!!! 그러나, 개념상의 미분을 완전히 구현할수는 없어서, 일련의 값을 넣어서, 매우 많이 계산함으로 모방을 한다!!.
예를들어, 사인함수 f(x) = sin(x), x=0.5에서의 f'(x)를 다음과 같이 계산한다.
integer i, imin, n<-30;
real error, y, x<-0.5, h<-1, emin<-1
for i = n
h <- 0.25h
y <- [sin(x+h)-sin(h)]/h
error <- |cos(x)-y|
output i,h,y,error
if error < emin then
emin<-error; imin<-i
endif
endfor
output imin, emin
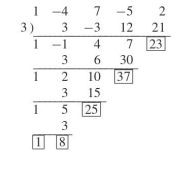
컴플리트 호너 알고리즘을 구현해봤다.
#include <iostream>
#include <vector>
using namespace std;
std::vector<int> Horner(const std::vector<int>& input, int r){
std::vector<int> res;
res.resize(input.size() - 1);
res[0] = input[0];
for(size_t i = 0; i < input.size() - 2; i++){
res[i + 1] = input[i + 1] + r * res[i];
}
return res;
}
std::vector<int> Horner_Complete(const std::vector<int>& input, int r){
std::vector<int> res = input;
for(size_t k = 0; k < res.size(); k++){
for(size_t i = 1; i < res.size() - k; i++){
res[i] = res[i] + r * res[i - 1];
}
}
return res;
}
auto main() ->int{
vector<int> a({ 1,-4,7,-5,2 });
vector<int> h = Horner_Complete(a, 3);
for(auto& ele : h){
cout << ele << endl;
}
}
'알고리즘 + 자료구조' 카테고리의 다른 글
| 트리 (0) | 2023.06.15 |
|---|---|
| Recursion(재귀) (0) | 2023.06.14 |
| Recursion - English Ruler (0) | 2023.06.14 |
| Singly Linked List (0) | 2022.10.17 |
| 순수 가우스 소거법 Naive Gaussian Elimination (0) | 2022.07.14 |